So,
Here we have the following right triangle:
Let's find the side "b" first.
We could use the trigonometric ratio: "tan(a)". Where "a" is an angle.
The ratio tan(a), represents the relation between the opposite side of the angle and its adjacent side.
So, we could write:
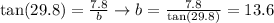
Therefore, b=13.6
The side "c" can be found if we apply the function sin(a). Where "a" represents an angle. This ratio relations the opposite side of the angle "a" and the hypotenuse of the triangle. Then, we could write:
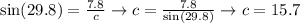
Therefore, c=15.7
Finally, to find the angle B we could use the fact that the sum of all internal angles of a triangle is always 180°. Therefore, we could write:
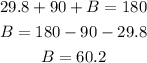
The angle B measures 60.2°.