1 Answer

Ranindu · Answer 1 · 2023-11-14T18:35:08+0000

Givens.

• Weight = 7,656 N.

,

• Initial speed = 43.13 km/h.

,

• Time = 9.38 seconds.

,

• Final speed = 0 km/h. (The car stops)

First, find the acceleration involved.

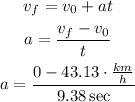
$\begin{gathered} v_f=v_0+at \\ a=(v_f-v_0)/(t) \\ a=(0-43.13\cdot(km)/(h))/(9.38\sec ) \end{gathered}$

But, we need to transform the initial speed to meters per second.

$43.13\cdot(km)/(h)\cdot\frac{1000m}{1\operatorname{km}}\cdot(1h)/(3600\sec)=11.98\cdot(m)/(s)$

Now we can proceed to find the acceleration.

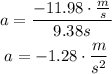
$\begin{gathered} a=(-11.98\cdot(m)/(s))/(9.38s) \\ a=-1.28\cdot(m)/(s^2) \end{gathered}$

Once you have the acceleration. Find the mass of the car using the weight formula.

$\begin{gathered} W=mg \\ 7,656N=m\cdot9.8\cdot(m)/(s^2) \\ m=(7,656N)/(9.8\cdot(m)/(s^2)) \\ m=781.22\operatorname{kg} \end{gathered}$

Then, use Newton's Second Law to find the needed force to stop.

$\begin{gathered} F=ma \\ F=781.22\operatorname{kg}\cdot(-1.28\cdot(m)/(s^2)) \\ F=-999.96N \end{gathered}$

Therefore, the magnitude of the force needed to stop the car is 999.96 Newtons.

Please log in or register to add a comment.