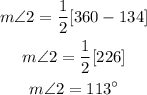From the first figure
Since LR and JV are 2 chords intersected at a point inside the circle, then
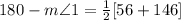
The angle next to <1 and form a line JV with it
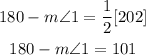
Add m<1 to both sides and subtract 101 from both sides
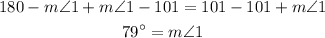
In the second figure
Since TU is a tangent to the circle at point T
Since ST is a chord in the circle
Then angle of tangency subtended by the major arc ST, Its measure is half the measure of the subtended arc.
Since the major arc ST = the measure of the circle - the measure of the minor arc ST
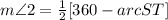
Since the measure of the minor arc ST is 134 degrees, then