The circumcenter of a triangle can be found as the intersection of the perpendicular bisectors of its sides.
It is enough to draw two perpendicular bisectors, since the third one will intersect the first two in the same point.
In this case, it is easier to find the perpendicular bisectors of the sides of the triangle which are parallel to the Y-axis and the X-axis, respectively.
The midpoint of the segment from (-4,2) to (-4,-3) is:
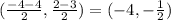
The line perpendicular to that segment that goes through (-4,-1/2) is given by the equation:
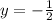
Using a similar procedure, we can find that the equation of the perpendicular bisector of the segment from (-4,-3) to (0,-3) is:

Those two lines intersect at the point:
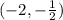
Which must be the circumcenter of the triangle.