Question

1. Todd purchased 2 CDs and 3 cassettes for $75. Paulena went to the same music stores and purchased 1 CD and 5 cassettes for $76. Find the cost of one CD and one cassette

Answer 1

Let D be the CDs and C for the cassetes. We can write the first statement as

`2D+3C=75`

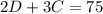
and the second statement as

`1D+5C=76`

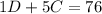
Then, we must solve these equations.

Solving by elimination method.

We can multiply by -2 the second equation. Then, we have the following system of equations:

`\begin{gathered} 2D+3C=75 \\ -2D-10C=-152 \end{gathered}`

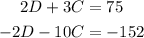
We can see that if we add both equations, we obtain

`3C-10C=75-152`

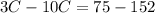
because 2D-2D=0. Then, we have

`-7C=-77`

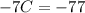
If we move the coefficient -7 of C to the right hand side, we have

`\begin{gathered} C=(-77)/(-7) \\ C=11 \end{gathered}`

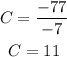
Now, we can substitute this value into the first equation in order to find D. It yields,

`\begin{gathered} 2D+3(11)=75 \\ 2D+33=75 \\ 2D=75-33 \\ 2D=42 \\ D=(42)/(2) \\ D=21 \end{gathered}`

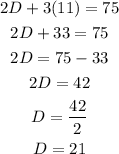
Then, the answer is C=11 and D=21. So, the cost for the CDS is $21 and for the cassettes is $11.