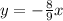If we have two perpendicular lines of slopes m₁ and m₂, then we have the following equation:
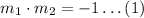
From the problem, we have the line with equation 9x - 8y = 10. The slope-intercept form of this line is:
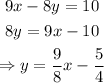
Then, the slope of this line is:
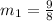
Using (1), we can find the slope of any perpendicular line to this line. Then:
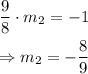
Additionally, we know that this line passes through the point (0, 0), so the point-slope form of the perpendicular line is:
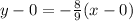
And the corresponding slope-intercept form is: