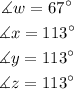Question

In the figure shown to the right, two parallel lines are cut by a third line. Find w, x, y, and z.

Answer 1

So first of all is important to note that angle y and the 113° angle are what is known as corresponding angles. Basically, the sides that define them are parallel which means that they have the same measure. Then:

`\measuredangle y=113^(\circ)`

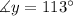
y and z are opposite angles. Just like before, one of the sides of y is parallel to one of the sides of z and the remaining sides are also parallel. Then they also have the same measure:

`\measuredangle z=\measuredangle y=113^(\circ)`

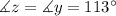
Using the same argument, x and the 113° have the same measure:

`\measuredangle x=113^(\circ)`

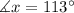
Finally, w and y are interior angles. This means that the sum of their measures must be equal to 180°. Then we get:

`\measuredangle y+\measuredangle w=113^(\circ)+\measuredangle w=180^(\circ)`

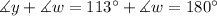
If we substract 113° from both sides of the last equality we get:

`\begin{gathered} 113^(\circ)+\measuredangle w-113^(\circ)=180^(\circ)-113^(\circ) \\ \measuredangle w=67^(\circ) \end{gathered}`

Then the answers are:

`\begin{gathered} \measuredangle w=67^(\circ) \\ \measuredangle x=113^(\circ) \\ \measuredangle y=113^(\circ) \\ \measuredangle z=113^(\circ) \end{gathered}`