Question

A line passes through the points (9,-4) and (10, -3). What is its equation in slope-interceptform?Write your answer using integers, proper fractions, and improper fractions in simplest form.

Answer 1

y = x - 13

Step-by-step explanation:

The equation of a line that passes through two points (x1, y1) and (x2, y2) is:

`y-y_1=m(x-x_1)`

Where m is calculated as:

`m=(y_2-y_1)/(x_2-x_1)`

So, replacing (x1, y1) by (9, -4) and (x2, y2) by (10, -3), we get that m is equal to:

`m=(-3-(-4))/(10-9)=(-3+4)/(1)=(1)/(1)=1`

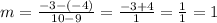
Then, the equation of the line is:

`\begin{gathered} y-(-4)=1(x-9) \\ y+4=x-9 \end{gathered}`

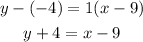
Finally, to write the equation in slope-intercept form, we need to solve for y, so:

`\begin{gathered} y+4-4=x-9-4 \\ y=x-13 \end{gathered}`

So, the answer is:

y = x - 13