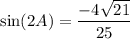Answer:
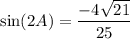
Explanation:
We are given that:
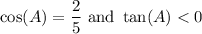
And we want to determine the value of:
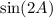
First, since cos(A) is positive and tan(A) is negative, this means that ∠A must be in QIV.
In QIV, cosine is positive, sine is negative, and tangent is also negative.
The given ratio tells us that the adjacent side to ∠A is 2, and the hypotenuse is 5.
Then by the Pythagorean Theorem, the opposite side will be given by:
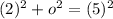
Solve for the opposide side:
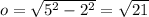
So, with respect to ∠A, the adjacent side is 2, the opposite side is √(21), and the hypotenuse is 5.
Using the double-angle identity, we can rewrite our original expression as:
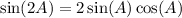
Using the above information, substitute in values. Remember that cosine is positive and that sine is negative:
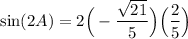
Simplify. Therefore: