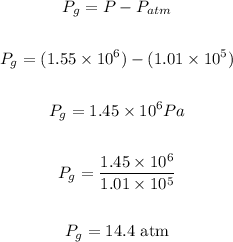Answer:
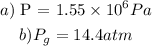
Step-by-step explanation:
The pressure needed to raise the boiling point of water to 200.0°C can be gotten from the graph of temperature versus saturation pressure of water
Checking from the graph:
The water pressure necessary to raise the boiling point to 200.0°C = 1554900 Pa

b) To calculate the gauge pressure, follow the steps below