To obtain the equation of the line that passes through these points, you can first obtain the slope of the line, using the formula
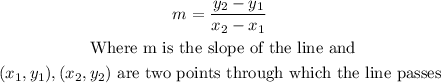
And then use the point-slope formula

So, in this case, you have

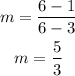
Now using the point-slope formula
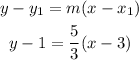
Therefore, the correct answer is D.
