Question

If f(n) = 4n + 7 and g(n) = 2n + 3, find (g - f)(n).2(n-4)4- 2n-2n - 42n + 4

Answer 1

The question provides two functions:

`\begin{gathered} f(n)=4n+7 \\ g(n)=2n+3 \end{gathered}`

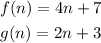
We are then told to find (g - f)(n).

Using the Operation of functions we can solve this problem.

`(g-f)(n)=g(n)-f(n)`

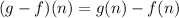
Since we know what g(n) and f(n) are, we can find (g - f)(n).

This is done below:

`\begin{gathered} (g-f)(n)=g(n)-f(n) \\ g(n)=2n+3 \\ f(n)=4n+7 \\ \\ \therefore(g-f)(n)=g(n)-f(n)=(2n+3)-(4n+7) \\ (g-f)(n)=2n+3-4n-7 \\ \\ \text{Collect like terms} \\ \\ (g-f)(n)=2n-4n-7+3 \\ \therefore(g-f)(n)=-2n-4 \\ \\ \end{gathered}`

Therefore, the final answer is:

-2n - 4