Given:
The perimeter of a rectangle is 44 meters.
The length is 10 meters more than twice the width.
Required:
To find the dimensions.
Step-by-step explanation:
The perimetero of rectangle formula is
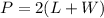
Let x be the width.
The length is 10 meters more than twice the width.
So
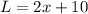
Now

Here the width is 4m.
Now the length is
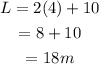
Final Answer:
18 meters and 4 meters.