Question

if
`(2)/(x + 1) + (8)/(y - 3) = (10)/(3)`and
`(4)/(x + 1) - (2)/(y - 3) = (2)/(3)` what is the value of x + y?

Answer 1

`x\text{ + y = 8}`

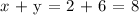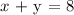
Here, we want to get the value of x + y

We proceed as follows;

From the second equation, we have that;

`(2)/(y-3)\text{ = }(4)/(x+1)-(2)/(3)`

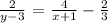
We can rewrite the first equation as;

`(2)/(x+1)+4((2)/(y-3))\text{ = }(10)/(3)`

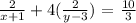
We substitute the first equation above in the second

Thus, we have that;

`\begin{gathered} (2)/(x+1)\text{ + 4(}(4)/(x+1)-(2)/(3))\text{ = }(10)/(3) \\ \\ (2)/(x+1)+(16)/(x+1)-(8)/(3)\text{ = }(10)/(3) \\ \\ (18)/(x+1)\text{ = }(10)/(3)+(8)/(3) \\ \\ (18)/(x+1)\text{ = }(18)/(3) \\ \\ x+1\text{ = 3} \\ x\text{ = 3-1} \\ x\text{ = 2} \end{gathered}`

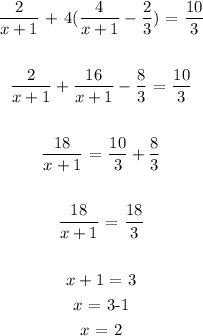
We then proceed to get the value of y by substituting the obtained value of x

We have this as;

`\begin{gathered} (2)/(y-3)\text{ =}(4)/(x+1)-(2)/(3) \\ \\ (2)/(y-3)\text{ = }(4)/(3)-(2)/(3) \\ \\ (2)/(y-3)\text{ = }(2)/(3) \\ \\ y-3\text{ = 3} \\ y\text{ = 3+ 3 = 6} \end{gathered}`

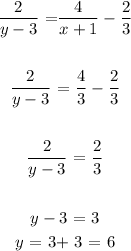
Thus, we have the value of x + y as;

`x\text{ + y = 2 + 6 = 8}`