Question

Find the measure of the arc or angle indicated. Assume that lines which appeartangent are tangent.Find mMPM12x + 3S45°РRQ3x + 12

Answer 1

Step-by-step explanation:

The arc MP, arc SQ, and angle MRP are related by the following equation:

`\angle MRP=(1)/(2)(MP-SQ)`

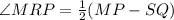
Then, replacing the expressions for each angle and arc, we get:

`3x+12=(1)/(2)((12x+3)-45)`

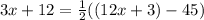
So, solving for x, we get:

`\begin{gathered} 3x+12=(1)/(2)(12x+3-45)_{} \\ 3x+12=(1)/(2)(12x-42) \\ 3x+12=(1)/(2)(12x)-(1)/(2)(42) \\ 3x+12=6x-21 \\ 3x+12+21=6x-21+21 \\ 3x+33=6x \\ 3x+33-3x=6x-3x \\ 33=3x \\ (33)/(3)=(3x)/(3) \\ 11=x \end{gathered}`

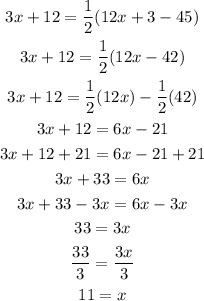
Now, with the value of x, we get that the measure of arc MP is equal to:

MP = 12x + 3

MP = 12(11) + 3

MP = 132 +3

MP = 135

Therefore, the answer is 135 degr