Question

7. The table below shows the amount spent on movie theater tickets in the U.S. from 1997 to 2003.YearSpending (billions of dollars)19976.319986.919997.920008.620019.020029.620039.9(a) Use a graphing calculator or spreadsheet program to find a quadratic model that best fits this data. Let t represent the year, with t=0 in 1997. Round each coefficient to two decimal places.Pt = (b) Based on this model, how much would you expect to be spent on movie theater tickets in 2008? billion dollars(c) When would you expect movie theater ticket expenditure to fall to $5 billion? Give your answer as a calendar year (ex: 1997).During the year

Answer 1

Step 1

Plot a graph of t representing the years where the first year 1997 is taken as 0 and other years follow consecutively against the spending in billions of dollars.

From the graph, the quadratic model that best fits the data with all coefficients rounded to 2 decimal places is

`P_t=-0.05t^2_1+0.91t_1+6.22`

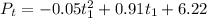
Step 2

Based on the model, find how much you would expect to be spent on movie theater tickets in 2008

`\begin{gathered} t_1=11 \\ P_t=-0.05(11)^2+0.91(11)+6.22 \\ P_t=-(121)/(20)+(1001)/(100)+6.22 \\ P_t=(509)/(50) \\ P_t=10.18\text{ billions of dollars} \end{gathered}`

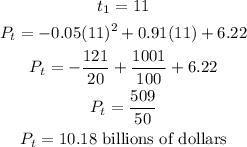
Step 3

Find when you would expect movie theater tickets to fall to $5 billion dollars.

`\begin{gathered} P_t=5 \\ 5=-0.05t^2+0.91t+6.22 \\ 5(\: 100)=-0.05t^2(\: 100)+0.91t(\: 100)+6.22(100) \\ 500=-5t^2+91t+622 \\ -5t^2+91t+622=500 \\ -5t^2+91t+622-500=500-500 \\ -5t^2^{}+91t+122=0 \\ Solve\text{ with the quadratic formula} \\ t_(1,\: 2)=\frac{-91\pm\sqrt[]{91^2-4\mleft(-5\mright)(\: 122)}}{2\mleft(-5\mright)} \\ \sqrt[]{91^2-4\mleft(-5\mright)(\: 122})=√(10721) \\ t_1=(-91+√(10721))/(2\left(-5\right)),\: t_2=(-91-√(10721))/(2\left(-5\right)) \\ t_1=-(-91+√(10721))/(10),\: t_2=(91+√(10721))/(10) \\ t_1=-1.25422619,t_2=19.45422619 \end{gathered}`

Since the value of t cannot be negative t is taken as 19.45422619

This means movie theater tickets will fall to $5 billion dollars in 19.45422619 years as required 19.45422619 years as a calendar year based on the question is during the year 2016

Answer to part C; During the year 2016