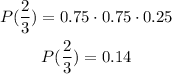ANSWER
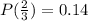
Step-by-step explanation
The probability that a plane will arrive on time is:
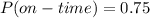
This means that the probability that a plane will not arrive on time is:
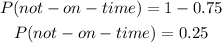
The probability that 2 out of 3 planes will arrive on time is the probability that 2 planes will arrive on time and that one will not arrive on time.
Therefore, we have to find the product of each probability: