Answer:
hello your question is incomplete attached below is the screenshot of the missing part
answer : The treatment had an effect on the growth of the trees
Step-by-step explanation:
H0 : No significant effect
Ha : At least one treatment has a significant effect
To confirm the above hypothesis ( conduct one way ANOVA )
From the one way Anova
( X represents each group; from control to Fertilizer and irrigation )
∑ X1^2 = 0.2338 , ∑ X2^2 = 1.8284, ∑X3^2 = 0.1982, ∑X4^2 = 11.8492
Also : ∑ N = 5 + 5 + 5 + 5 = 20 where N = number of trees in each group
also K represents number of groups i.e. = 4
Next calculate the sum of squares ( calculated using online tools )
i) Between sum of squares: value = 4.6824
ii) Within sum of squares : value = 4.3572
Next step : Calculate the degrees ( DF)
i) Between degrees of freedom
Dfb = k - 1 where K = 4 therefore Dfb = 3
ii) within degrees of freedom
Dfw = N - k , where N = 20 and K = 4 therefore Dfw = 16
Next : calculate mean sum of squares
i) Between mean sum of squares
= 4.6824 / 3 = 1.5608
ii) within mean sum of squares
= 4.3572 / 16 = 0.2723
Calculate the F-statistic value
 = Between mean sum of squares / within mean sum of squares
= Between mean sum of squares / within mean sum of squares
= 1.5608 / 0.2723 = 5.73
determine the F critical value
Fcritical =
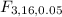 = 3.2389 ( obtained from F table )
= 3.2389 ( obtained from F table )
since
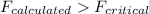 hence we can say The treatment had an effect on the growth of the trees i.e. Reject H0
hence we can say The treatment had an effect on the growth of the trees i.e. Reject H0