ANSWER
Step-by-step explanation
First, we have to fill in the table with the y-values. To do so, we have to plug the x-values in the function and solve,
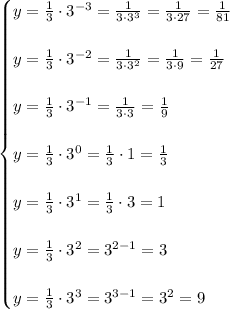
So the table is,
Then, we have to graph each of these points in the coordinate plane. The first two or three points will not be accurate because they are very small values and the scale of the y-axis is too big,
And, finally, we join the dots with a curve to sketch the graph of the function.