Question

The table represents some points on the graph of a linear function. Which equation represents the same relationship?A: y-3=-2(x+6)B: y-6 = - 1/2 (x+3)C: y+3=-1/2(x-6)D:y-6=-2(x+3)

Answer 1

To determine which of the options best defines the table, we will have to determine the equation of the line that defines the table.

To find the equation of a line

let us select the first two points of the table

`\begin{gathered} \text{when } \\ x=-4,\text{ y=2} \\ \text{when} \\ x=-2,\text{ y=1} \end{gathered}`

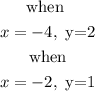
We can now use the equation of the line formula

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ \\ (y-2)/(x-(-4))=(1-2)/(-2-(-4)) \\ \\ (y-2)/(x+4)=(1-2)/(-2+4) \\ \\ (y-2)/(x+4)=(-1)/(2) \end{gathered}`

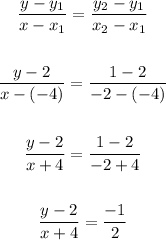
The next step will be

to cross multiply

`y-2=-(1)/(2)(x+4)`

To find the option that conforms to the expression

`\begin{gathered} \text{let us add 5 to both sides} \\ y-2+5=-(1)/(2)(x+4)+5 \\ \\ y+3=-(1)/(2)x-2+5 \\ y+3=-(1)/(2)x+3 \\ \text{This is equivalent to} \\ y+3=-(1)/(2)(x-6) \end{gathered}`

ThusThe correct answer is option C