Question

Which of the following sets of side lengths, in inches, will form a triangle? A. 3.5, 7.2, and 3.0B. 3.2, 5.9, and 4.5C. 10.0, 4.6, and 5.3D. 5.5, 4.9, and 10.5

Answer 1

In order to see which sides form a triangle, we can apply the triangle inequality theorem:

Case A.

In this case, we can choose a=3.5, b=7.2 and c=3. By applying the inequalities, we get

`\begin{gathered} 3.5+7.2>3\Rightarrow10.7>3\text{ Thats correct } \\ 3.5+3>7.2\Rightarrow6.5>7.2\text{ thats incorrect !} \end{gathered}`

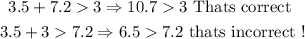
Then, these segments doesnt form a triangle.

Case B.

In this case, we can choose a=3.2, b=5.9 and c=4.5. By applying the inequalities, we get

`\begin{gathered} 3.2+5.9>3\Rightarrow9.1>3\text{ Thats correct } \\ 3.2+4.5>5.9\Rightarrow7.7>5.9\text{ Thats correct } \\ 5.9+4.5>3.2\Rightarrow10.2>3.2\text{ Thats correct } \end{gathered}`

Then, these segments can make a triangle

Case C.

In this case, we can choose a=10, b=4.6 and c=5.3. By applying the inequalities, we get

`\begin{gathered} 10+4.6>5.3\Rightarrow14.6>5.3\text{ Thats correct } \\ 10+5.3>4.6\Rightarrow15.3>4.6\text{ Thats correct } \\ 4.6+5.3>10\Rightarrow9.9>10\text{ Thats incorrect } \end{gathered}`

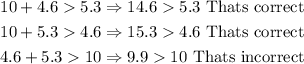
Then, these segments doesnt form a triangle.

Case D.

In this case, we can choose a=5.5, b=4.9and c=10.5. By applying the inequalities, we get

`5.5+4.9>10.5\Rightarrow10.4>10.5\text{ Thats incorrect }`

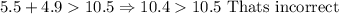
Then, these segments doesnt form a triangle.

Therefore, the answer is option B.