To find the x-intercept(s), we can use the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
This formula is applied when we have a polynomial of the form:

We have that our case is:
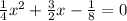
To find the x-intercepts of the parabola. However, we can find the least common multiple of the denominators to have an easier equation to solve. Then, we have:
![\operatorname{lcm}(4,2,8)=8]()
Then, we can multiply each side of the equation by 8 as follows:
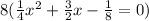
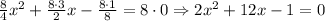
Now, we have that:
a = 2
b = 12
c = -1
Then, we have:
![x=\frac{-12\pm\sqrt[]{12^2^{}-4(2)(-1)}}{2\cdot2}](https://img.qammunity.org/2023/formulas/mathematics/college/yi2hz0t6rriydqo303ypiewmf3iryg4ykc.png)
![x=\frac{-12\pm\sqrt[]{144+8}}{4}\Rightarrow x=\frac{-12\pm\sqrt[]{152}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/f1k4scopf3j2t9eqhtcna2nsgww73ji44u.png)
Then
![\sqrt[]{152}=\sqrt[]{2^2\cdot2\cdot19}=2\cdot\sqrt[]{38}](https://img.qammunity.org/2023/formulas/mathematics/college/hewg8ak77f3iwas0w8hgxhyxvskyp4zxtd.png)
Then, the two x-intercepts are:
![x=\frac{-12\pm2\cdot\sqrt[]{38}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/h82xdcmf597mjin6gd0vt4cen8k92owkje.png)
![x=\frac{-12+2\cdot\sqrt[]{38}}{4}\Rightarrow x=-(12)/(4)+\frac{2\cdot\sqrt[]{38}}{4}=-3+\frac{\sqrt[]{38}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/w5ngyatj55cd0yrjnobiiyhy112xbto6kf.png)
And
![x=\frac{-12-2\cdot\sqrt[]{38}}{4}\Rightarrow x=-(12)/(4)-\frac{2\cdot\sqrt[]{38}}{4}=-3-\frac{\sqrt[]{38}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/le16607uq8qdmv2s5de9dnginyyb9qrht3.png)
Therefore:
The smallest x-intercept is:
![-3-\frac{\sqrt[]{38}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/fy9vae1sbhvhh60pqwrevbhiwk3m92a9kh.png)
The largest x-intercept is:
![-3+\frac{\sqrt[]{38}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/cmxyibiqzp1q7k1d92qpyukeshtvdnlcwe.png)
Finding the value of the vertex
To find the vertex of the parabola, we can find its x-value, and y-value using the following formulas:

In the original equation, we have:
a = 1/4
b = 3/2
c = -1/8
Then, we have:
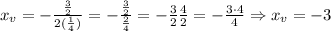
And
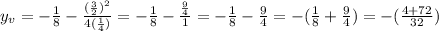
Finally:

Therefore, the vertex of the parabola is:
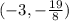
In summary, we have:
The coordinates for the vertex are:
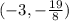
The smallest x-intercept (only the