Question

In the diagram of ACFE below, GD||FE, CG=10, CD=12, and DE=72. What is the length of CF? С 10 12 G D 72 Do F E Spomit Arcus Answet Type here to search O

Answer 1

In the given triangle FCE and GCD

angle C is common

as line GD || FE

angle EFC = angle DGC (corresponding angle)

Similarly

Angle CDG = AngleCEF (Corresponding angle)

By Angle Angle similarity, triangle FCE and GCD are similar

From thr properties of similar triangle,

The ratio of corresponding sides of similar triangle are equal

`\begin{gathered} In\text{ }\Delta FCE\text{ \&}\Delta\text{ GCD} \\ (FC)/(GC)=(CE)/(CD)=(EF)/(DG) \end{gathered}`

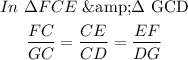
substitute the value: GC = 10, CD = 12, DE = 72

as: CE = CD + DE

CE = 12 + 72

CE = 84

`\begin{gathered} (FC)/(GC)=(CE)/(CD)=(EF)/(DG) \\ (FC)/(10)=(84)/(12)=(EF)/(DG) \end{gathered}`

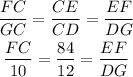
For the length CF, simplify first two expression:

`\begin{gathered} (CF)/(10)=(84)/(12) \\ CF=(84*10)/(12) \\ CF=7*10 \\ CF=70 \end{gathered}`

Answer : CF = 70