The increasing interval of a function can be founded by taking the derivative of the function and then calculating where the derivative is possitive.
We have the function:

The derivative, by the chain rule is:
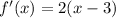
Now we need to find the interval where the derivative is possitive. Let's find the root:
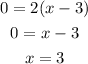
The derivative is 0 when x = 3. Now lets evaluate the derivative in a number greater than 3, if it's possitive, the increasing interval will be (3,∞) If it's negative, the interval will be (-∞, 3)
Let's evaluate for x = 4:
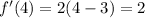
Then, the increasing interval is (3,∞)