Question

How many combinations are possible? Assume the items are distinct.9 items chosen 7 at a time________ combinations

Answer 1

To solve this question, we use the combination formula.

The combination formula is

`^nC_r=(n!)/(r!(n-r)!)`

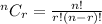
Where n represents the amount of items in the set, and r represent the amount of items we want to select from this set.

For our problem, we have

`n=9,r=7`

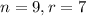
Then, the combinations are given by

`^9C_7=(9!)/(7!(9-7)!)`

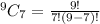
Solving this we have

`\begin{gathered} ^9C_7=(9!)/(7!(9-7)!) \\ ^9C_7=(9\cdot8\cdot7!)/(7!(2)!) \\ ^9C_7=(9\cdot8)/(2!) \\ ^9C_7=(9\cdot8)/(2) \\ ^9C_7=9\cdot4 \\ ^9C_7=36 \end{gathered}`

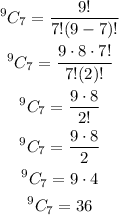
We have 36 combinations.