Final answer:
The consumer's surplus under pure competition is $5.62.
Step-by-step explanation:
The consumer's surplus is the difference between the price that consumers are willing to pay for a product and the price they actually pay. To find the consumer's surplus under pure competition, we need to find the equilibrium quantity and price where the demand and supply curves intersect.
First, we set the demand and supply equations equal to each other: 28/(x + 1) = 1 + 0.2x.
Next, we solve for x:
28 = (1 + 0.2x)(x + 1)
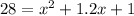
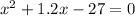
Using the quadratic formula, we get two possible values for x: x = 4.57 or x = -5.57. Since the number of units can't be negative, we discard the negative value.
Therefore, x = 4.57.
Now, we can find the price at this equilibrium quantity by plugging x into either the demand or supply equation. Let's use the supply equation: p = 1 + 0.2x = 1 + 0.2(4.57) = 2.91.
The consumer's surplus is the difference between the maximum price consumers are willing to pay (the demand equation) and the equilibrium price: (28/(x + 1)) - 2.91 = (28/(4.57 + 1)) - 2.91 = 5.62.
So, the consumer's surplus under pure competition is $5.62.