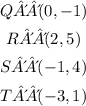We need to find the following operation
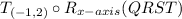
which means that we need to find first the reflection over the x-axis of the figure QRST:
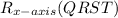
and then translate the result 1 unit left and 2 units up:
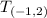
In this regard, the rule for a reflection over the x-axis is given by
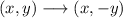
Then, by applying the reflection rule, we have that
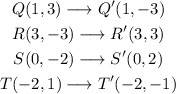
Now, the translation rule for 1 units to the left and 2 units up
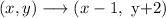
Then, by applyin this rule to the last result, we have
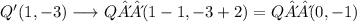
and
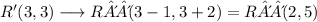
and
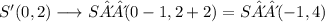
and finally,
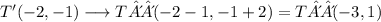
Therefore, the answer is: