Let's call x the mL of the 14% solution that we are going to use.
Then the number of mL in the mixture will be (x+6)mL.
Thus, the equation will be:
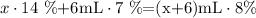
14%=0.14
7%=0.07
8%=0.08
Now, we have to solve for x:
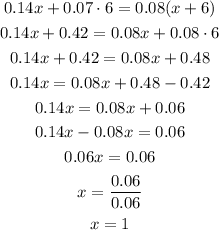
Let's check:
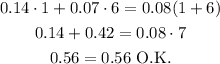
Answer: 1 mL of the 14% medication solution is needed to make a final