Alana makes soup and packages it in conical containers that each have a height of 5 inches. What is the radius of each container of a pack of 12 containers contains 203.5 inches…

Question

asked Jun 25, 2023 175k views

1 Answer

JMarques · Answer 1 · 2023-07-01T01:47:31+0000

We are given that 12 cones contain 203.5 cubic inches. Since there a re 12, the volume of each individual cone is:

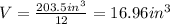
Now, the volume of a cone is given by the following formula:

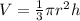
$V=(1)/(3)\pi r^2h$

Where "r" is the radius and "h" the height. Solving for the radius first by multiplying by 3:

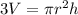
$3V=\pi r^2h$

Now we divide both sides by pi:

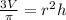
$(3V)/(\pi)=r^2h$

Now we divide both sides by "h":

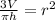
$(3V)/(\pi h)=r^2$

Now we take the square root to both sides:

$\sqrt[]{(3V)/(\pi h)}=r$

Now we replace the known values:

$\sqrt[]{(3\mleft(16.96in^3\mright))/(\mleft(3.14\mright)\mleft(5in\mright))}=r$

Solving the operations:

$\sqrt[]{(50.88in^2)/(15.7)}=r$
$\sqrt[]{3.2in^2}=r$
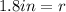
1.8in=r

Therefore, the radius is 1.8 inches.