Given:
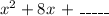
Let's find the number that will make the expression a perfect trinomial.
To find the number, apply the formula:
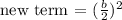
From the expression:
b = 8
Hence, we have:
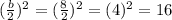
Therefore, the number that will make the expression a perfec squaret trinomial is 16 .
Hence, the trinomial is:
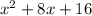
ANSWER:
16