Question

 find a reference angle to five pie over eight and fill in the calculations as well

Answer 1

alpha = PI - 5/8 PI

alpha = 3/8 PI

The angle 5/8 Pi is found in the second quadrant.

The reference angle for any angle (A) in the second quadrant is given by

`\begin{gathered} A_r=180-A \\ \\ A_r=\pi-A\text{ (In radian)} \end{gathered}`

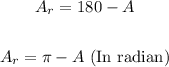
Therefore, we can solve for 5/8 Pi:

`\begin{gathered} A_r=\pi-(5)/(8)\pi \\ \therefore A_r=(3)/(8)\pi \end{gathered}`

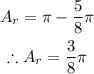
But in order to put it in the box in the question:

`\begin{gathered} \alpha=PI\text{ - }(5\pi)/(8) \\ \\ \alpha=(3)/(8)\text{ PI} \end{gathered}`

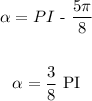
alpha = PI - 5/8 PI

alpha = 3/8 PI