Question

Point C is midpoint of segment AB for A (1, -2) and B (7,2). What is the length of segment AC? Round to the nearest tenth.

Answer 1

To find the point C, we need to use the formula for the midpoint:

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

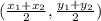
Then the point C is:

`C=((7+1)/(2),(2+(-2))/(2))=((8)/(2),(0)/(2))=(4,0)`

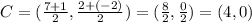
therefore, the point C is (4,0).

Now that we find the point C, we need to use the formula:

`d(P,Q)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

to find the length of the segment AC:

`\begin{gathered} d(A,C)=\sqrt[]{(4-1)^2+(0-(-2))^2} \\ =\sqrt[]{(3)^2+(2)^2} \\ =\sqrt[]{9+4} \\ =\sqrt[]{13} \\ =3.6 \end{gathered}`

Therefore, the length of the segment AC is 13.