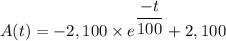Answer:
The number A(t) of pounds of salt in the tank at time 't' is;
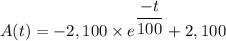
Explanation:
In the question, we have;
The volume of pure water initially in the tank = 700 gal
The concentration of brine pumped into the tank = 3 pounds per gallon
The rate at which the brine is pumped into the tank, = 7 gal/min
The rate at which the well mixed solution is pumped out = The same 7 gal/min
The number of pounds of salt in the tank at time 't' is found as follows;
The rate of change in A(t) with time = The rate of salt input - The rate of salt output
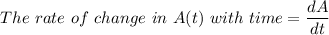
The rate of salt input = 7 gal/min × 3 lbs/gal = 21 lbs/min
The rate of salt output = (A(t)/700) lb/gal × 7 gal/min = (A(t)/100) lb/min
Therefore, we have;
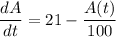
Therefore;
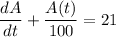
The integrating factor is
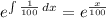
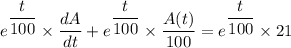
![(d)/(dt) \left[ e^{(t)/(100) } *{A(t)}{} \right]= e^{(t)/(100) } *21](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/y4g8ierjp40yt1o8wc5fnw.png)
Using an online tool, we get;
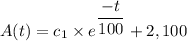
At time t = 0, A(t) = 0
We get;
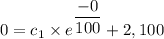
c₁ = -2,100
Therefore, the number A(t) of pounds of salt in the tank at time 't' is given as follows;