Given the exponential function:
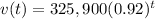
to find the initial value of the house, we can make t = 0 and evaluate on v(t):
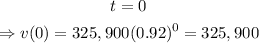
then, the initial value of the house is $325900
Notice that the rate factor on the function is 0.92, which, since it is less than 1, shows a decay rate.
Finally, since the decay factor is 0.92, we have that the house each year losses 100-92=8% of its value