Step 1
All radiation decay follows first order kinetics as follows:
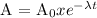
λ = decay constant
t = time taken
A0 = initially present mass
A = mass present after t time
------------------
Step 2
Information provided:
12.3 y = half-life time = t 1/2
A0 = 48.0 mg
-------------------
Step 3
Procedure:
λ is calculated as follows:
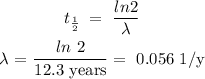
Now,
From step 1:
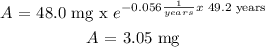
For t = 98.4 years => A = 0.194 mg
Answer:
What mass of the nuclide will remain after 49.2 y? 3.05 mg
And then after 98.4 y? 0.194 mg