We know that the wind is blowing from north to south with a speed of 32 km per hour, let's call the wind vector W, then it can be written as
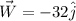
We also know that Diane wants the plane to fly north of east at an angle of 25° and a speed of 140 km/h. This means that the resultant should be
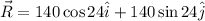
Now, we would like to know at what angle Diane should fly tha plane. To find this we will introduce a vector T whose magnitud and direction are unknown.
Then
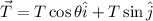
Now, we know that the resultant is
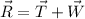
then
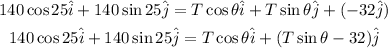
Since the unit vector i and j are independent this gives us two equations
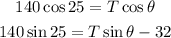
From the first equation we have that
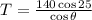
Plugging the value of T in the second equation we have
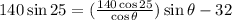
Now we need to solve this equation for theta.
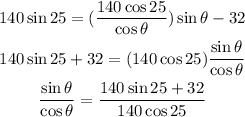
Now we have to remember that
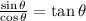
hence
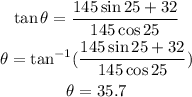
Therefore Diane has to direct the airplane at an angle of 35.7° North of east.