Answer: The behavior of the function can be checked by finding the derivative of it and evaluating it at the two specified points:
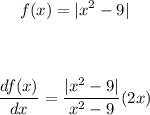
The behaviour at x = -3 and x = 3.
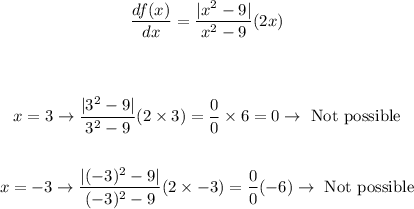
The answer therefore is:
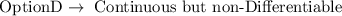
Plot for the function:
Not that the f(x) is indeed Differentiable function
, but there can not be any slope at x = -3 and x = 3.