Question

Find the real solutions for t:36t^4 + 33t^2 – 3 = 0

Answer 1

You have the following equation:

`36t^4+33t^2-3=0`

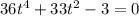
In order to solve for t, first divide by 3 both sides:

`12t^4+11t^2-1=0`

use the quadratic equation for t^2, as follow:

`\begin{gathered} t^2=\frac{-11\pm\sqrt[]{(11)^2-4(12)(-1)}}{2(12)} \\ t^2=(-11\pm13)/(24) \\ t^2=(-11+13)/(24)=(2)/(24)=(1)/(12) \\ t^2=(-11-13)/(24)=(-24)/(24)=-1 \end{gathered}`

If you only consider real solutions for t, then, you obtain two real solutions from t^2=1/12.

Then, the solutions are:

`t=\frac{1}{\sqrt[]{12}},t=-\frac{1}{\sqrt[]{12}}`