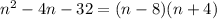Question

This is a practice assignment. This factoring quadratics, algebra 1.

Answer 1

To factor a quadratic polynomial of the form:

`n^2+bn+c`

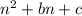
we need to find to intergers B and C that fulfill the following conditions:

`\begin{gathered} BC=c \\ \text{and} \\ B+C=b \end{gathered}`

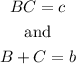
In the case of the polynomial:

`n^2-4n-32`

we notice that b=-4 and c=-32. Then we need to find two numbers that fulfills:

`\begin{gathered} -32=BC \\ -4=B+C \end{gathered}`

if we choose B=-8 and C=4 we notice that this requierements are fulfill. Once we have this numbers we write the polynomial as:

`n^2-8n+4n-32`

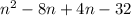
and we factor the first two terms and the last two terms by common factors:

`\begin{gathered} n^2-4n-32=n^2-8n+4n-32=n(n-8)+4(n-8) \\ =(n-8)(n+4) \end{gathered}`

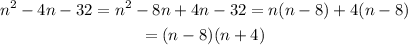
Therefore:

`n^2-4n-32=(n-8)(n+4)`