Given inequalities are
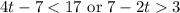
Consider

Adding 7 on both sides, we get
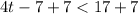

Dividing both sides by 4, we get

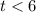
Consider
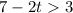
Subtracting 7 from both sides, we get
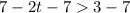
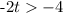
Dividing both sides by (-2), and reverse the inequality since we divide by negative number.

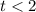
Hence the answer is
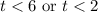
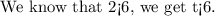
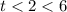
The interval notation of the solution is
