To shift the graph of a function f(x) in a units in the horizontal axis, we replace x by x - a:
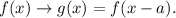
To shift the graph of a function f(x) in b units in the vertical axis, we sum b to the function:
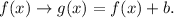
------------------------------------------
We have the parent function:
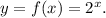
The transformed function is:
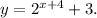
1) First, we shift the function f(x) a = -4 units in the horizontal axis, we get:
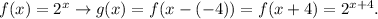
2) Secondly, we shift the function g(x) b = 3 units in the vertical axis, we get:
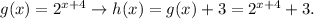
We see that the transformed function h(x) is obtained by shifting f(x):
0. a = -4 units in the horizontal axis, i.e. ,4 units to the left,,
,
1. b = 3 units in the vertical axis, i.e. ,3 units up,.
Answer
C. Shifted left 4 and up 3