Question

Please view images and use the graph to complete questions

Answer 1

A function is increasing on an interval if the function values( y values) increase as the input values(x-values ) increase within that interval.

For the graph giving, the function increases at the given point

hence

The function increases at the interval

`\begin{gathered} (-9,-6) \\ (0,5) \\ \text{and } \\ (8,\infty) \end{gathered}`

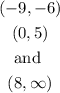
The right option is given in the image below

b.) The local minima is the point where the function has the smallest y coordinate.

Hence, from the image above, the local mminima is at the point

`(-9,-3),(0,-9)\text{ and (}8,-6)`

Hence, the x-values are

`x-\text{values :-9,0,8}`

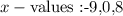
Therefore

The x-values are -9,0,8

C). The Leading coeffiient is obtain from the right hand side of the graph.

From the graph given, the end of the graph function towards the right is moving upward which is in the positive direction,

Hence, The leading coefficient is

`\text{Positive}`

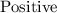
Answer: The leading Coefficient is Positive

D). An n-degree polynomial has atleast

`(n-1)\text{ turning and n x-intercept }`

From the graph above,

`\begin{gathered} \text{Number of turning point =5} \\ Number\text{ of x-intercept =2} \end{gathered}`

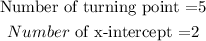
The maximum number of turning points of a polynomial function is always one less than the degree of the function.

The minimun degree of the polynomial is 6

The polynomial is atleast of degree 6

The Answer is; 6,7,8,9