We are given the following geometric series
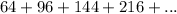
Common ratio:
The common ratio (r) of a geometric series can be found as
r = 96/64 = 1.5
you can take any two consecutive terms, the common ratio will always be the same
r = 144/96 = 1.5
r = 216/144 = 1.5
Therefore, the common ratio of the given geometric series is 1.5
Now let us find the sum of the first 10 terms of this series.
The sum of a geometric series is given by
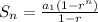
Where a₁ is the first term of the series, r is the common ratio, and n is the number of terms.
For the given case
a₁ = 64
r = 1.5
n = 10
Let us substitute these values into the above formula

Therefore, the sum of the first 10 terms of this series is 7253.12