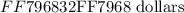Question

Lexi deposited $20 in a savings account earning 10% interest, compounded annually.To the nearest cent, how much interest will she earn in 3 years?Use the formula B = P(1 + r), where B is the balance (final amount), p is the principal(starting amount), r is the interest rate expressed as a decimal, and t is the time in years.

Answer 1

We will investigate the application of simple interest on any amount saved.

Lexi deposited an initial principal ( P ) amount in her saving's account. We will write down the initial savings as follows:

`\textcolor{#FF7968}{P}\text{\textcolor{#FF7968}{ = \$20}}`

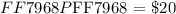
A saving's account is a contract between the user and the bank which is signed for certain amount of interest rate ( R ). This interest rate ( R ) defines at what percentage the initially savings ( P ) will be compounded. In this simplest terms its an "extra value added" over the initial saving.

We will go ahead and express the rate ( R ) that was signed by Lexi as interest:

`\textcolor{#FF7968}{R}\text{\textcolor{#FF7968}{ = 10\%}}`

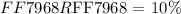
To determine the actual amount of simple interest earned by Lexi pertains to the time period ( t ) over which account balance is to be evaluated. This is a contractual time period given as follows:

`\textcolor{#FF7968}{t}\text{\textcolor{#FF7968}{ = 3 years}}`

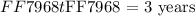
The above three are parameters for determining the simple interest ( I ) for any initial principal amount ( P ) at an interest rate ( R ) compounded annually for a contractual time period ( t ). We can mathematically express the simple interest ( I ) as follows:

`\begin{gathered} I\text{ = }(P\cdot R\cdot t)/(100)\text{ } \\ \textcolor{#FF7968}{I}\text{\textcolor{#FF7968}{ = P}}\textcolor{#FF7968}{\cdot r\cdot t\ldots}\text{\textcolor{#FF7968}{ Eq1}} \end{gathered}`

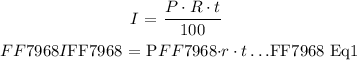
Once we have evaluated the " extra amount " we will add this amount to Lexi's initial deposit ( P ) and determine the her account balance after the contractual period as follows:

`\text{\textcolor{#FF7968}{Lexi Account Balance = Simple Interest ( I ) + P }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq2}}`

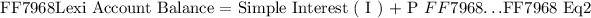
Now we will combine the two expression ( Eq1 and Eq2 ) as follows:

`\begin{gathered} \text{Lexi Account Balance = P}\cdot r\cdot t\text{ + P} \\ \text{\textcolor{#FF7968}{Lexi Account Balance = P}}\textcolor{#FF7968}{\cdot(1+r\cdot t)}\text{\textcolor{#FF7968}{ }} \end{gathered}`

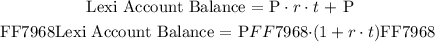
Now we will use the above expression to determine Lexi's account balance after contractual period. We will plug in the respective quantities as follows:

`\begin{gathered} \text{Lexi Account Balance = }20\cdot(\text{ 1 + }(20)/(100)\cdot3) \\ \\ \text{Lexi Account Balance = }20\cdot(\text{ 1.6}) \\ \text{\textcolor{#FF7968}{Lexi Account Balance = \$32 }} \end{gathered}`

Therefore Lexi's account balance after 3 years is:

`\textcolor{#FF7968}{32}\text{\textcolor{#FF7968}{ dollars}}`