Looking at the orientation of each figure, first we need a reflection over the y-axis, this way the orientation of ABCD will match the orientation of EHGF.
After this reflection, the position of each point will be:
(To find the position after a reflection over the y-axis, we need to switch the signal of the x-coordinates)
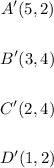
Now, let's write the coordinates of EHGF:
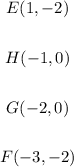
Comparing each corresponding pair of points, we can see that in order to map A'B'C'D' into EHGF, we need to decrease the x-coordinates by 4 units and decrease the y-coordinates by 4 units:
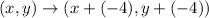
Therefore the answers are y, -4 and -4.