SOLUTION
Write out formula
Where
PMT= Monthly payment
P= Principal
APR= Annual payment rate
n = number of times compounded in a year
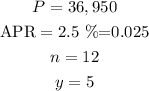
Substitute the values into the formula
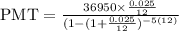
Simplifying the expression above
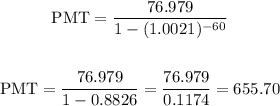
Hence
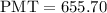
Therefore,
Andre will need to save 655.70monthly to reach his goal