Given: Force 12N and 14N
To Determine: The strength and the direction of the resultant
Solution
The strength of the given is the magnitude of the resultant
The result is R in the diagram above
Using Pythagoras theorem
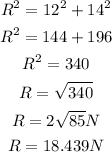
From the diagram
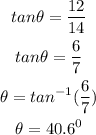
The direction of the resultant is
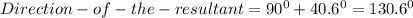
Hence:
The strength of the resultant is 18.4N
The direction of the resultant is 130.6⁰