Solution
- The equation modeling the height of the falling object is:
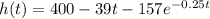
Question 1:
- To find the velocity of the falling object, we simply differentiate the function with respects to time (t).
- After this, we can find when the velocity of the object is -30ft/s by substituting V = -30 and find the value of t.
- Thus, we have:
![\begin{gathered} h(t)=400-39t-157e^(-0.25t) \\ \\ h^(\prime)(t)=(d)/(dt)(h(t))=(d)/(dt)(400-39t-157e^(-0.25t)) \\ \\ h^(\prime)(t)=-39-157(-0.25)e^(-0.25t) \\ \\ h^(\prime)(t)=V(t)=-39+39.25e^(-0.25t) \\ \\ \text{ Now that we have the expression for }V(t),\text{ we can proceed to find when the velocity is -30 by making }V(t)=-30 \\ \\ -30=-39+39.25e^(-0.25t) \\ \text{ Add 39 to both sides} \\ 39.25e^(-0.25t)=39-30=9 \\ \\ \text{ Divide both sides by 39.25} \\ \\ e^(-0.25t)=(9)/(39.25) \\ \\ \text{ Take the natural log of both sides} \\ \\ -0.25t=\ln((9)/(39.25)) \\ \\ \text{ Divide both sides by -0.25} \\ \\ t=-(1)/(0.25)\ln((9)/(39.25)) \\ \\ t=5.890907...\approx5.89s \end{gathered}]()
- The time is 5.89s
Question 2:
- The height of the object at time t = 5.89s is gotten by substituting this value of time (t) into the equation of the height given to us.
- We have:
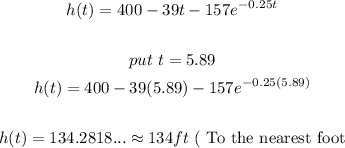
- the height is 134 ft