Question

Graph each equation using the intercepts. 3x-2y=-8

Answer 1

We have the next equation

`3x-2y=-8`

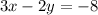
And we must graph it using the intercepts.

So, we must find the x and y intercept

x intercept:

To find the x intercept we must replace y = 0 in the function and then solve it for x

1. Replacing y = 0

`3x-2(0)=-8`

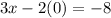
2. Solving for x

`\begin{gathered} 3x-0=-8 \\ 3x=-8 \\ x=(-8)/(3)=-2.67 \end{gathered}`

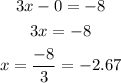
So, the x intercept is (-2.67, 0)

y intercept:

To find the y intercept we must replace x = 0 in the function and then solve it for y

1. Replacing x = 0

`\begin{gathered} 3(0)-2y=-8 \\ -2y=-8 \\ y=(-8)/(-2) \\ y=4 \end{gathered}`

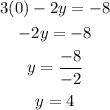
So, the y intercept is (0, 4)

Finally, the graph of the function will be the line that passes through the two intercepts