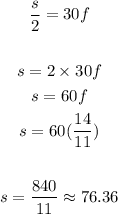Question

Some were fast, and the rest were slow. Ten times the number of fast was 140 less than twice the number of slow. Also, one-half the number of slow exceeded 3 times the number of fast by 10. How many were fast and how many were slow?

Answer 1

we write an equation for each statement

Ten times the number of fast was 140 less than twice the number of slow

`10f=2s-140`

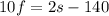
Also, one-half the number of slow exceeded 3 times the number of fast by 10

`\begin{gathered} (s)/(2)=3f*10 \\ \\ (s)/(2)=30f \end{gathered}`

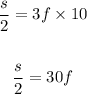
where f is the number of fast and s the numer of slow

Now we can solve one unknow from any equation and replace on the other equaiton

for example:

I will solve s from the second equation

`\begin{gathered} (s)/(2)=30f \\ \\ s=2*30f \\ s=60f \end{gathered}`

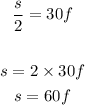
and replace s on the other equation

`\begin{gathered} 10f=2s-140 \\ 10f=2(60f)-140 \\ 10f=120f-140 \end{gathered}`

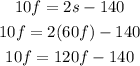
now we place the terms with f on the same side

`10f-120f=-140`

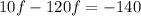
simplify

`\begin{gathered} (10-120)f=-140 \\ -110f=-140 \\ 110f=140 \\ \\ f=(14)/(11)\approx1.27 \end{gathered}`

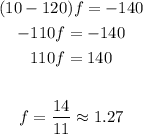
the number of fast was 1.27

now the number of slow we can check it if we replace f on any equation, for example on the Second

`\begin{gathered} (s)/(2)=30f \\ \\ s=2*30f \\ s=60f \\ s=60((14)/(11)) \\ \\ s=(840)/(11)\approx76.36 \end{gathered}`